Nell'epoca di macchine che fanno tutto da sole e che non lasciano al fotografo che l'incombenza di scattare, non è male andare a rispolverare gli elementi base dell'ottica, per cercare di non dimenticare quali siano le basi "vere" della nostra professione o del nostro hobby. Da vero esperto della materia, Davide Dassio ci guida nel regno della luce e delle leggi dell'ottica.

Fig. 1

Fig. 2
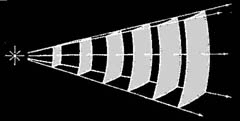
Fig. 3
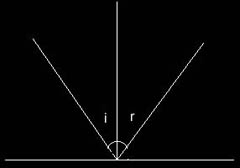
Fig. 4
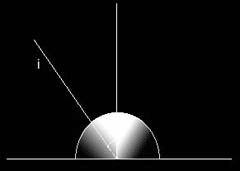
Fig. 5

Fig. 6
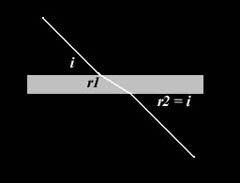
Fig. 7
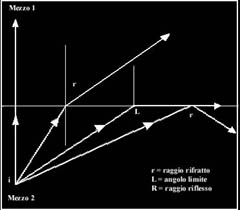
Fig. 8
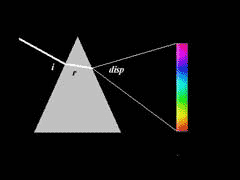
Fig. 9
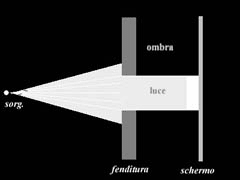
Fig. 10

Fig. 11
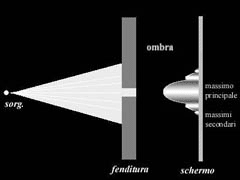
Fig. 12

Fig. 13
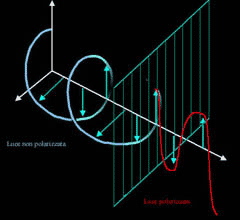
Fig. 14
Natura della luce
La luce è una radiazione elettromagnetica costituita da un ciclico alternarsi di campi elettrici e magnetici di intensità variabile secondo legge sinusoidale (fig.1); la luce visibile ha una lunghezza d'onda compresa tra i 380 nm (nanometri) del violetto e i 750 nm del rosso (fig.2); si propaga in linea retta, in tutte le direzioni sotto forma di fronti d'onda sferici aventi centro nella sorgente che li ha generati (fig.3), con velocità inversamente proporzionale alla densità del mezzo attraversato. Da ciò consegue che tanto più la distanza dalla sorgente aumenta, tanto maggiore è il raggio di curvatura del fronte d'onda; i fronti d'onda intercettati a distanza dalla sorgente da oggetti molto più piccoli possono essere considerati aventi superficie piana, e il raggio di luce che unisce la sorgente al fronte d'onda intercettato (o all'oggetto che lo intercetta), una linea retta. Queste sono le basi dell'ottica geometrica.
La riflessione della luce
Ogni corpo, si a esso opaco oppure trasparente, emette luce. Quando la luce viene riflessa da un corpo di dimensioni macroscopiche con superficie liscia (ad esempio uno specchio) allora la riflessione della luce che si ottiene (per definizione speculare e ideale) segue la legge della riflessione: il raggio riflesso giace sullo stesso piano formato dal raggio incidente e dalla normale al piano di incidenza; l'angolo di incidenza è uguale all'angolo di riflessione (fig.4), secondo la formula ai = ar. Se la superficie è scabra la luce viene riflessa in modo diffuso e nel caso ideale segue la legge di Lambert o del coseno: la luce viene riflessa in tutte le direzioni con intensità che decresce in ragione del coseno a partire dalla normale indipendentemente dall'angolo di incidenza (fig.5), secondo la formula In = Ia * cos(a), dove In è l'intensità della luce diffusa in direzione perpendicolare alla superficie; Ia è l'intensità della luce per un determinato angolo di riflessione; a è l'angolo di riflessione. Se la superficie è un corpo nero (ideale) la luce viene assorbita completamente indipendentemente dall'angolo di incidenza. Per i corpi reali i tre fenomeni descritti (riflessione, diffusione e assorbimento) sono sempre presenti contemporaneamente. Per la legge di conservazione dell'energia, la somma delle intensità della luce riflessa, sia in modo speculare che diffusa, e di quella assorbita è uguale all'intensità del raggio incidente, secondo la formula Ii = Ir + Ia. Diversamente si comporta la luce quando colpisce corpi microscopici: se la dimensione delle particelle è superiore alla lunghezza d'onda della luce, questa viene sempre diffusa; se la dimensione delle particelle è inferiore alla lunghezza d'onda della luce (come nel caso dell'aria) la luce viene diffusa in ragione della quarta potenza della lunghezza d'onda (questo è il motivo per cui il cielo di giorno è azzurro).
La rifrazione della luce
La rifrazione dipende dalla variazione di velocità che la luce subisce nel passare attraverso mezzi trasparenti di densità diversa. Il rapporto tra le velocità di propagazione della luce all'interno dei due mezzi è costante; in particolare il rapporto tra le velocità di propagazione della luce nell'aria e nel mezzo definisce l'indice di rifrazione di quel mezzo (fig.6), secondo la formula n1 = Va / V1 (dove n1 è l'indice di rifrazione, Va la velocità nell'aria e V1 quella nel mezzo). E' esperienza comune che un oggetto posto tra aria e acqua appaia tanto più spostato quanto più è inclinato. La legge di Snell quantifica il fenomeno:
n1 * sen(i) = n2 * sen(r)
(dove n è l'indice di rifrazione nel mezzo 1 e 2, i l'angolo di incidenza e r quello di rifrazione). Se il primo mezzo è l'aria, n1 = 1; ne deriva che l'inclinazione del raggio rifratto aumenta all'aumentare del raggio di incidenza e, a parità di angolo di incidenza, all'aumentare dell'indice di rifrazione:
n2 = sen(i) / sen(r) oppure: sen(r) = sen(i) / n2
Nell'attraversare un mezzo trasparente con superfici piane (diottro piano) la luce subisce due modificazioni nella sua velocità di propagazione: la prima nel passaggio dal primo mezzo al secondo, la seconda in uscita dal secondo mezzo nel primo. Allo stesso modo il raggio inclinato subirà una deviazione angolare nel passaggio attraverso il secondo mezzo per riassumere l'inclinazione originaria in uscita (fig.7). In realtà quando un raggio di luce incide su una superficie piana di un mezzo trasparente si verificano contemporaneamente una riflessione e una trasmissione (rifrazione) del raggio la cui intensità dipende dall'intensità e dall'angolo del raggio incidente (nella maggior parte dei casi i fenomeni della diffusione e dell'assorbimento sono trascurabili). In particolare l'intensità del raggio riflesso, nulla con raggio incidente perpendicolare alla superficie, aumenta all'aumentare del raggio di incidenza; il contrario avviene per il raggio rifratto la cui intensità diminuisce all'aumentare dell'angolo del raggio incidente. Da quanto espresso e dalla già citata legge si Snell consegue che fintanto che l'indice di rifrazione del mezzo in cui la luce incide è minore di quello in cui il raggio è rifratto la rifrazione è possibile; quando invece l'indice di rifrazione in cui il raggio di luce incide è maggiore di quello in cui è rifratto, a partire da un determinato angolo (detto angolo limite) si avrà una totale riflessione (fig.8). Per esempio nel caso di una lastra piana in vetro la rifrazione sarà sempre possibile nel passaggio aria/vetro, ma la luce potrà subire una riflessione nel passaggio tra vetro e aria. Il calcolo dell'angolo limite si ottiene risolvendo la legge di Snell rispetto all'angolo di incidenza (ovvero l'angolo limite), per l'angolo di rifrazione a 90° (fig.8):
n1 * sen(i) = n2 * sen(90) ; i = arcsen(n2/n1)
per n1 = 1 (aria) ; i = arcsen(n2)
Quando un raggio di luce attraversa un prisma (cioè un blocco di vetro a facce inclinate) viene deviato da due superfici non parallele le cui normali non sono perpendicolari; la deviazione finale dipende dall'angolo al vertice del prisma, dal suo indice di rifrazione e dall'angolo di incidenza del raggio:
d = ai(n-1)
dove d è la deviazione; ai è l'angolo di incidenza e n l'indice di rifrazione.
Al passaggio di un raggio di luce bianca attraverso un prisma si verifica anche il fenomeno della dispersione dei colori (fig.9): il raggio di luce uscente dal prisma, oltre che deviato, risulta scomposto nei vari colori dell'arcobaleno (ovvero nelle varie lunghezze d'onda della luce visibile); ciò dipende dal fatto che l'indice di rifrazione di un mezzo diottrico varia (seppur di poco) al variare della lunghezza d'onda della luce. Per esempio il vetro Crown ha un indice di rifrazione per l'azzurro uguale a 1,594 e per il rosso uguale a 1,569.
La diffrazione
Il fenomeno della diffrazione descrive il comportamento della luce quando questa incontra un ostacolo sul suo cammino; consiste in una deviazione dalla traiettoria rettilinea che verrebbe seguita in assenza di ostacoli. Se un raggio luminoso attraversa un fenditura e si proietta su uno schermo posto dietro di essa, si osserva una zona illuminata corrispondente alla fenditura separata nettamente da una zona d'ombra corrispondente allo schermo (fig.10). Questa situazione è vera fintantoché la larghezza della fenditura è molto maggiore della lunghezza d'onda della luce incidente.
Quando la luce attraversa una fenditura circolare di dimensioni note, su uno schermo posto dietro di essa si osservano delle frange circolari alternativamente chiare e scure poste attorno ad un massimo di intensità luminosa centrale (fig.11). Il valore di intensità del primo anello scuro (=0) e di quelli chiari laterali (detti massimi secondari) sono strettamente dipendenti dal rapporto tra la lunghezza d'onda della luce e il diametro del foro: se il foro è molto più grande della lunghezza d'onda (l) i massimi secondari sono talmente addossati a quello centrale da non essere distinguibili da esso (fig.12); se la lunghezza d'onda della luce è uguale al diametro della fenditura gli anelli secondari diventano chiaramente distinguibili (fig.11); se, ancora, la lunghezza d'onda della luce è minore del diametro della fenditura si ha un illuminamento diffuso nella cui porzione centrale va a cadere la maggior parte (84%) dell'intensità luminosa, e la fenditura si comporta come una singola sorgente di onde sferiche (dette secondarie). I fenomeni di diffrazione sono causa dei limiti degli strumenti ottici; in particolare il potere risolutivo degli strumenti in questione è determinato dalla dimensione del diaframma (nel caso di obiettivi fotografici) o della lente frontale (nel caso di microscopi).
Ricordiamo che per potere risolutivo o risolvente si intende il più piccolo angolo che possono formare i raggi emessi dalle sorgenti luminose quando passano attraverso una fenditura affinché i massimi principali di diffrazione possano essere risolti, cioè quando il massimo centrale di una figura di diffrazione coincide con il primo minimo dell'altra.
La polarizzazione
La luce emessa dalle normali sorgenti luminose non è polarizzata in quanto costituita da onde elettromagnetiche che oscillano in tutti i piani perpendicolari alla direzione di propagazione della luce (fig.13). Se un materiale polarizzante è interposto al fascio di luce normale, viene attraversato solo da quelle onde che sono polarizzate parallelamente all'asse di polarizzazione del materiale (fig.14). Il materiale interposto produce così luce polarizzata in un determinato piano e per questo viene definito filtro polarizzatore. L'intensità dell'onda trasmessa (It) dal polarizzatore dipendente dall'intensità dell'onda incidente (Ii) e dall'angolo q compreso fra la direzione di polarizzazione del polarizzatore e il piano di polarizzazione della luce incidente mediante la relazione (legge di Malus):
It = Ii * (cos(q))^2
In natura si ha polarizzazione della luce quando questa viene riflessa da superfici d'acqua (e vetro) o quando viene diffusa dalle molecole dell'aria. La polarizzazione ottenuta per riflessione è sempre parziale. A prova di ciò basta osservare che ruotando un filtro polarizzatore anteposto alla luce proveniente da uno specchio di acqua, l'intensità della luce varierà al ruotare del filtro (secondo la legge di Malus), ma non si otterrà mai il buio totale per la contemporanea presenza di radiazione luminosa non polarizzata.
Davide Dassio © 03/2005
Riproduzione Riservata