Per capire il significato di questi numeri risaliamo all'origine dei diaframmi. Come sappiamo, per un dato tempo di otturazione l'esposizione viene regolata raddoppiando o dimezzando l'area del diaframma. Assegnato il valore 1 all'area il cui diametro è uguale alla lunghezza focale, la aree, e di conseguenza l'esposizione, diminuiscono secondo la sequenza
1 - 1/2 - 1/4 - 1/8 - 1/16 - 1/32 - 1/64 - 1/128 - 1/256 - 1/512
E poiché l'area è proporzionale al quadrato del diametro, possiamo esprimere la stessa relazione in termini di quest'ultimo, sostituendo ai denominatori le rispettivi radici quadrate. Se arrotondiamo questi valori per motivi di praticità ritroviamo la nota serie dei diaframmi
1 - 1/1.4 - 1/2 - 1/2.8 - 1/4 - 1/5.6 - 1/8 - 1/11 - 1/16 - 1/22
In entrambi i casi i denominatori assumono i valori di una funzione esponenziale in base 2, rispettivamente alla potenza x ed x/2, e per valori interi di x.
Se per esigenze di precisione vogliamo dividere gli intervalli in 10 parti dobbiamo attribuire ad x i valori 0.1, 0.2, 0.3, ecc. ecc.
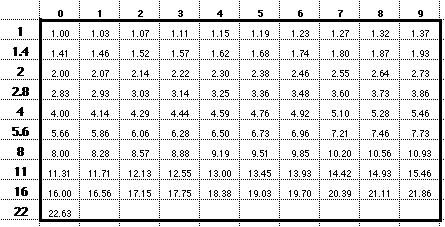
Tab. 1

Tab 2
Con un foglio di calcolo è un gioco calcolare i valori intermedi dei diaframmi, che ritroviamo nella tabella 1, e delle corrispettive aree nella tabella 3.
I valori intermedi dei diaframmi non sono molto utili, perché non disponiamo di metodi di regolazione così accurati. Diverso è il caso se, per esempio, vogliamo usare l'esposimetro come un densitometro, perché per ogni coppia diaframma-valore frazionale misuriamo la quantità di luce relativa all'apertura f/1. Così ad f/8 - 6 e ad f/11 - 9 la luce misurata è rispettivamente 1/97.01 ed 1/239 della luce ad f/1.
Questa tabella ci indica anche con precisione che 1/3 e 2/3 di stop corrispondono con buona approssimazione ai valori frazionali 4 e 7.
Romano Sansone © 02/2004
Riproduzione Riservata